Web 计算机图形学(上)
Categories: Study
序
来自 vczh 某计算机图形学问题的回答:
程序员的三大浪漫:操作系统、图形学、编译原理,学了都是用来给你开眼界的。这些都不是什么你不学就怎么样的课程,而是你想成为大牛,不学不行=_,=
Web 前端技术中和图形学挂钩的大致是 CSS3 的动画变换、SVG、Canvas、WebGL 这一些东西,但是前端工程师大多只停留在上层 API 操作方面,对于图形学的原理,譬如 GPU、图像的表示、图像几何变换的原理、纹理、层次模型等可能不是很了解。
在整理完SVG 新司机开车指南后,对底层的一些技术有一些兴趣,加上对这一块属于空白区,故花了几天时间对图形学基本进行学习,记录于此。
本文主要包括如下内容:
GPU
概念和历史
Graphics Processing Unit(GPU),即图形处理器, 是一种专门在个人电脑、工作站、游戏机和一些移动设备上运行绘图运算工作的微处理器。
GPU 相关概念在 20 世纪 70 年代末就已经被提出,使用单片集成电路(monolithic)作为图形芯片,当时就已经被用于视频、游戏、动画方面,可以很快的对几张图片进行合成(也就只有这个功能…);
到 80 年代末,基于数字信号处理芯片(digital signal processor chip)的 GPU 被研发出来,与前代相比速度更快、功能更强,但是价格很贵;
到 1998 年 NVIDIA 公司宣布 modern GPU 的研发成功,标志着 GPU 研发的历史性突破成为现实。modern GPU 使用晶体管(transistors)进行计算,在微芯片(microchip)中,GPU 所使用的晶体管已经远远超过 CPU。
之后就是一代一代的 modern GPU 被研制出来,且功能、运行速度不断增强。
GPU VS CPU
可能有人会问,我们已经有 CPU 用来解释计算机指令以及处理计算机软件中的数据了,为什么还要使用 GPU 呢? 要解释这个可以从 CPU 和 GPU 的结构说起。
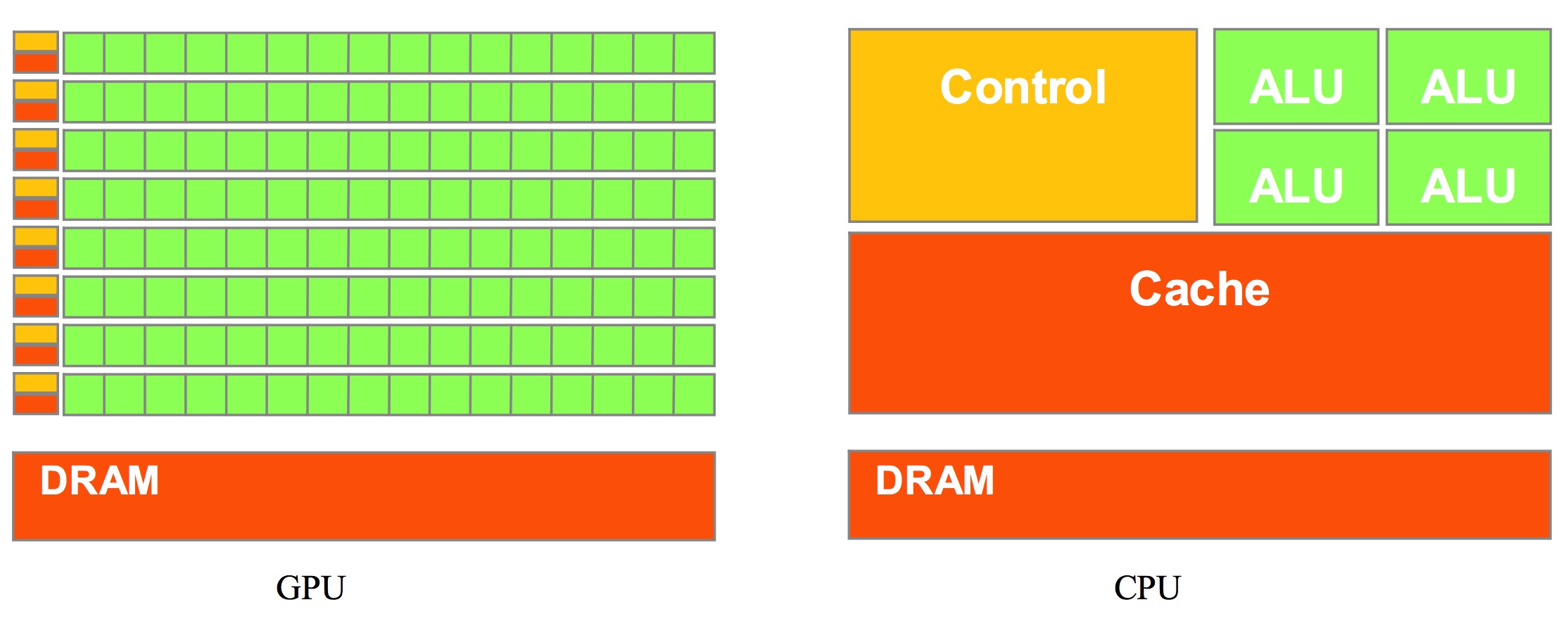
图片来自 NVIDIA CUDA 文档。其中绿色的是计算单元,橙红色的是存储单元,橙黄色的是控制单元。
从上图可以看到,GPU 基于大的吞吐量设计的,采用了数量众多的计算单元和超长的流水线,但只有非常简单的控制逻辑并省去了 Cache,在计算密集型的程序和易于并行的程序运行上有很大的优势;
CPU 基于低延时的设计,有强大的 ALU(算术运算单元),结构上不仅被 Cache 占据了大量空间,而且还有有复杂的控制逻辑和诸多优化电路,相比之下计算能力只是 CPU 很小的一部分。
CPU 的缩写是 Central Processing Unit, GPU 是 Graphics Processing Unit,表面可以理解为一个是公交司机,另外一个是专车司机,但是其实 GPU 相比 CPU 工作技术含量要低,用于计算量大、相比 CPU 技术含量低、重复很多次的工作。有人把 CPU 比作老教授,将 GPU 比作小学生,教授处理复杂任务的能力是碾压小学生的,但是对于没那么复杂的任务,还是顶不住人多的(有一种黑的味道…
汇总起来就是这样:
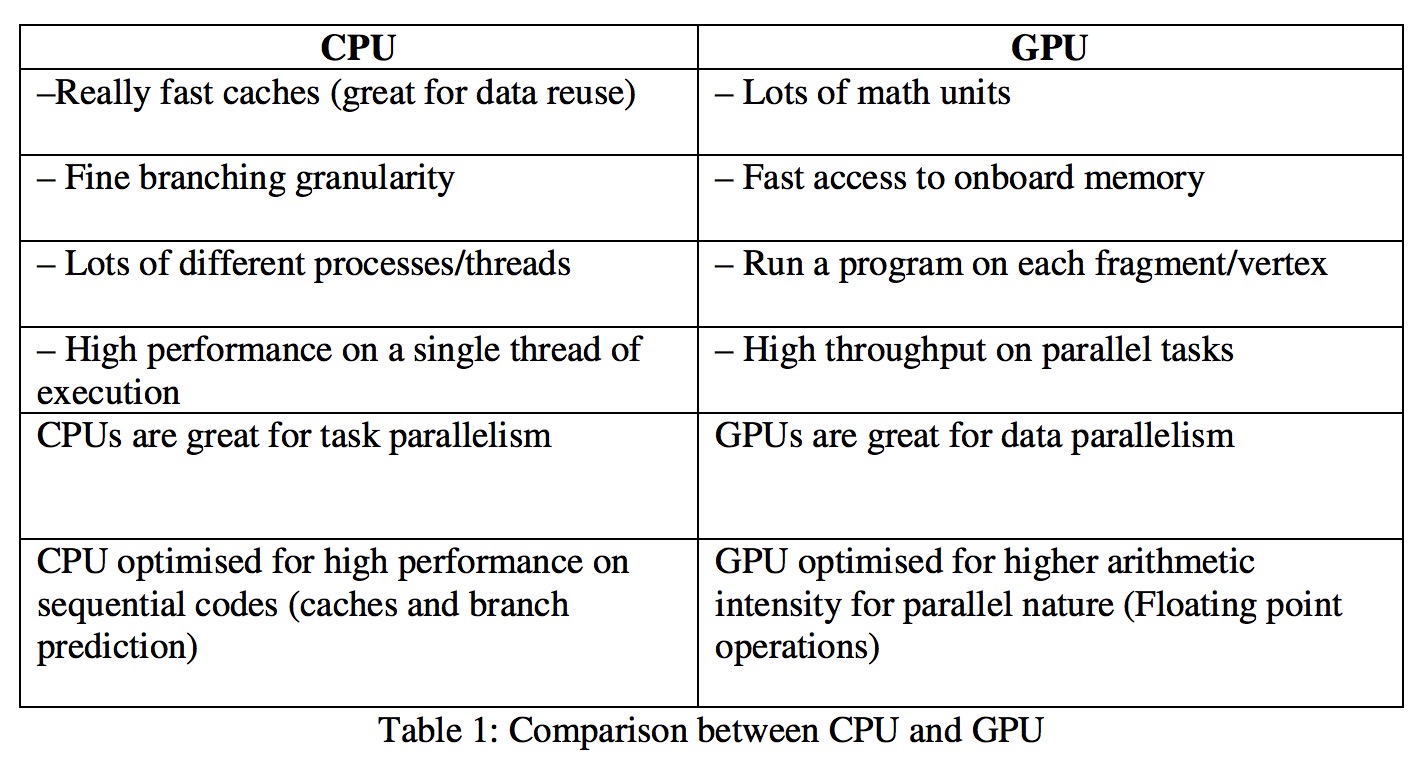
前端中的硬件加速
关于前端中的硬件加速其实是创建一个 Composited Layer 来开启 GPU 硬件加速,通过 GPU 进行渲染,解放 CPU,创建 Composited Layer 具体有如下方法:
- 3D 或透视变换(perspective transform)CSS 属性.
- 使用视频加速解码的<video>元素.
- 拥有 3D (WebGL) 上下文或加速的 2D 上下文的<canvas>元素
- 混合插件(如 Flash)
- 对自己的 opacity 做 CSS 动画或使用一个动画 webkit 变换的元素
- 拥有加速 CSS 过滤器的元素
- 元素有一个包含复合层的后代节点(换句话说,就是一个元素拥有一个子元素,该子元素在自己的层里)
- 元素有一个 z-index 较低且包含一个复合层的兄弟元素(换句话说就是该元素在复合层上面渲染)
在 chrome 中可以这样打开 Composited Layer:

图像表示
简介
什么是计算机图像学呢?在Computer graphics (disambiguation)上面是这么说的:
Computer graphics are graphics created by computers and, more generally, the representation and manipulation of pictorial data by a computer.
也即 计算机图形学是由计算机创建的图形,更普遍地说是计算机对图形数据的表示和操作。
在这章中主要理清图片是如何通过数据和特定的数据格式来表示的,同时说明计算机中颜色是如何表示的?
假设我们想将我们看到的美景保存下来,通常都是将其拍成照片,考虑到存储成本,我们必须将其转换成一个有限大小 数字形式的模拟信号,这个转换的过程即抽样。抽样理论也是 GC 中一个比较重要的内容,此处有时间再详细讨论。
照片中我们看到的信息相比现实场景中所包含的信息肯定会小很多,同时也不会像现实中那样无限宽高,从而我们必须在准确性方面进行妥协,通过选用适当的方法来采样和存储我们的图像。
光栅图象表示
计算机图形学解决图像表示问题的方法是将图像(图片)分割成规则网格,我们称之为栅格。每个网格单元是一个“图像单元”,一个常与像素收缩的术语。像素是图像的原子单位,也即一个单一颜色体。
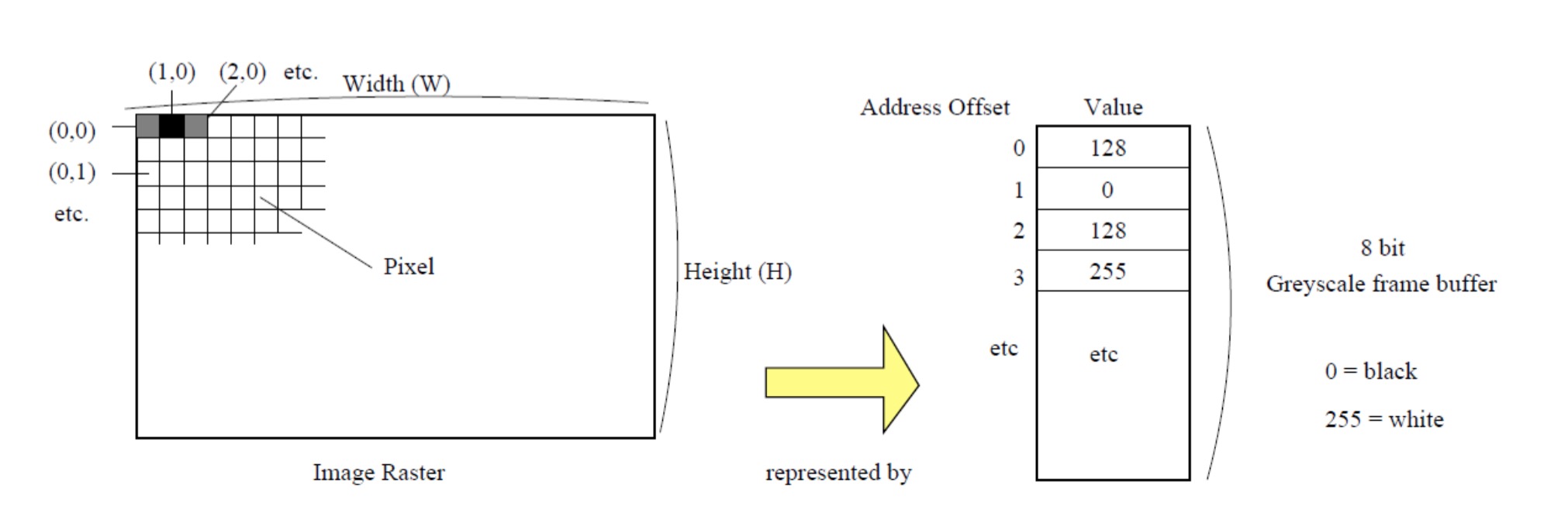
上图,通过光栅来表示数字图像,光栅说明这里有一个灰色图像,它的内容在内存中表示的灰度帧缓冲。存储在帧缓冲区中的值记录在离散刻度上的像素的强度(0 =黑色,255 =白色)。
我们平时所说的屏幕分辨率即图像中像素的数目,分辨率越大,图像的空间细节就越大。
帧缓冲器
我们用一个结构化的方法来存储每个像素的颜色值来表示一个图像。
帧缓冲最初的定义是指内存保留直接操作当前显示的图像。在早期的图形,需要特殊的硬件来存储足够的数据来代表的只是单一的形象。但是现在我们可以在内存中同时操纵成百上千的图片,从而“帧缓冲”逐渐用来描述任何一块代表一个图像的存储。
现在常见的帧缓冲有灰度帧缓冲、伪彩色帧缓冲、真彩色帧缓冲这三种。
灰度帧缓冲是最简单形式的一种,通过使用各种灰度梯度来编码像素。使用 8 位将像素编码为无符号整数,来表示 256 种不同的灰度阴影。
伪彩色帧缓冲是一种存储方案和灰度帧相同,但是可以用来表示彩色图像,也即 0−255 中每一个代表着一种特定的颜色,而不是代表灰色阴影。
真彩色帧缓冲也用来表示彩色图像,但是不是像伪彩色帧缓冲那样通过查找表的方式来表示颜色,而是将每个像素的 RGB 颜色值直接存储在帧缓冲区。如果我们使用 8 位(1 字节)来表示红色,绿色和蓝色特定颜色,那么每个像素将需要 24 位(3 字节)的存储空间。
颜色的表示
要想搞明白颜色,我们可以首先了解下我们的眼睛。
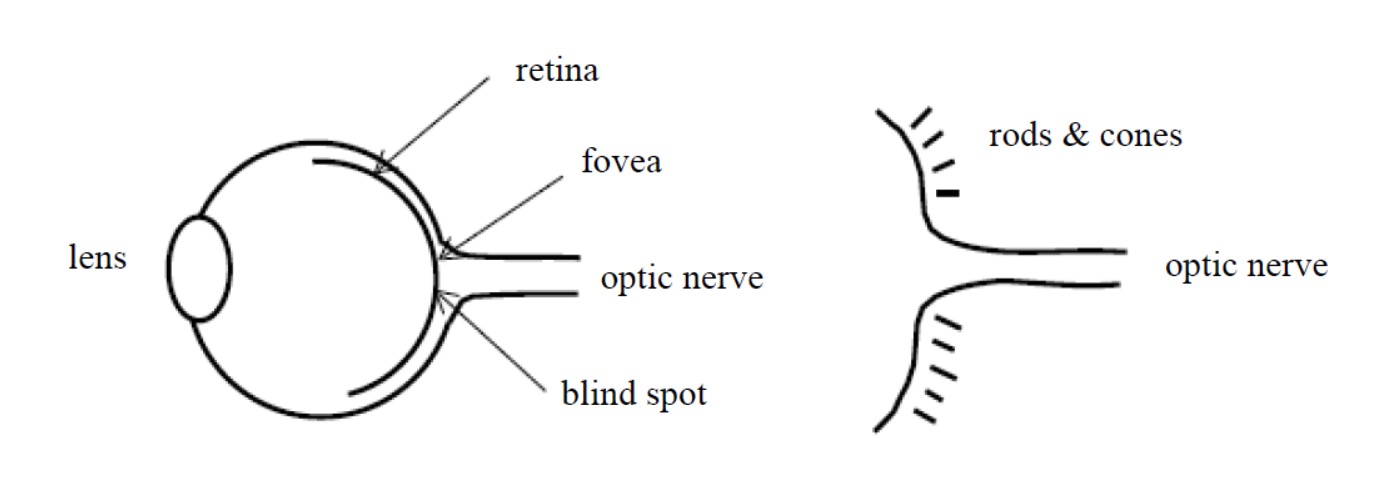
看图说话是这样的:
- lens :弹性透镜,我们眼睛通过它将光聚焦到视网膜;
- retina :视网膜,视网膜中有 fovea,是视网膜中视力最高的部分,是 rods 细胞和 cones 细胞的集中区,这两种特殊细胞(棒和锥)可以将光信息转换成电脉冲;
- optic nerve :视神经,转换成电脉冲的光信息通过视神经传到我们的大脑;
- blind spot :盲点,不含感光细胞的地方;
cones 锥细胞负责色觉,它有三种类型的圆锥体,都已经发展到对特定波长的光(蓝色、绿色、红色)有很高的敏感度。
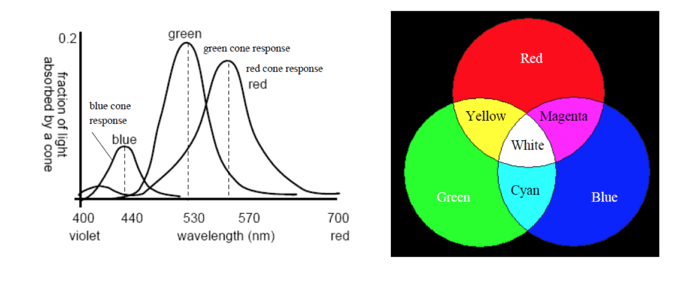
红色,绿色和蓝色被称为“加法原色”,可以通过将不同数量的红,绿和蓝光叠加来获得其他的颜色。
RGB 颜色表示法
在上图中我们可以看到 Red+Green=Yellow,在前端中表示颜色通常使用 HEX 方式或者 RGB 方式,黄色表示为#FFFF00 或者 rgb(255,255,0)。那么为什么可以看到黄色呢?我们可以理解成,那个黄色的物体其实最不喜欢黄色,它将其他光都吸收了,将黄色反射出来了,从而黄色的窄波段光波进入了我们的眼睛,刺激了红色和绿色的圆锥体细胞,所以我们感觉物体是黄的。
前端中 rgba 表示颜色也比较常见,它是 RGB 色彩模型的一个扩展。这个缩写词代表红绿蓝三原色的首字母,Alpha 值代表颜色的透明度/不透明度,取值为 0-1。
HSL 颜色表示法
除了用 RBG 来表示颜色,还可以颜色三要素来表示,也即 HSL 颜色表示法,其中包含如下:
- Hue:色相,指的是色彩的外相,是在不同波长的光照射下,人眼所感觉不同的颜色,如红色、黄色、蓝色等,这些颜色分布在一个平面的色相环上,取值范围是 0° 到 360° 的圆心角,每个角度可以代表一种颜色。
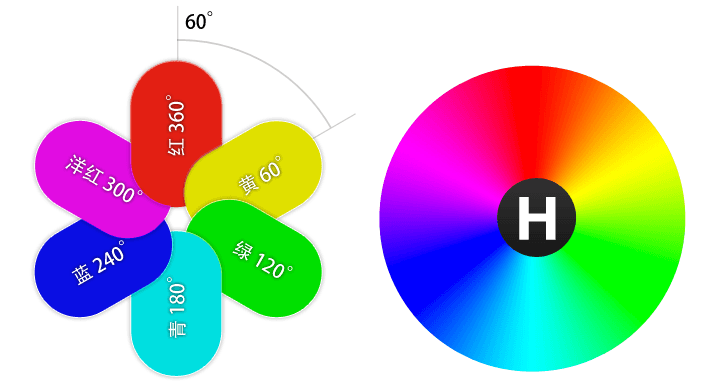
- Saturation:饱和度,指色彩的纯度,越高色彩越纯,低则逐渐变灰。

- Lightness:明度,又称亮度,指的是颜色的明暗。

同时也有 hsla,可以对比上述 rgba。
关于 RGB 和 HSL 的快速切换可以通过 chrome 来实现,按住 shift 再点击即可切换。
此外还有 HSV 来表示颜色,即色相、饱和度、明度(英语:Hue, Saturation, Value),又称 HSB,其中 B 即英语:Brightness。
几何变换
几何变换和 CSS3 中的 transform 变换相关,本节主要是从数学方面来给 transform 变换原理。
几何变换有时也被称为刚体变换, 即图形中所有的点均是在同一个变换下进行,可以从下图来区别是否为刚体变换:

其中图 2 经过图 1 反射得到、图 3 经过图 1 进行缩放和旋转组合的方式得到,然后图 4 是经过图一的枕形畸变(pin-cushion distortion)非刚体变换得到,请注意,只有刚体变换可以使用矩阵乘法来实现。
首先我们可以来复习下线性代数中的矩阵乘法:
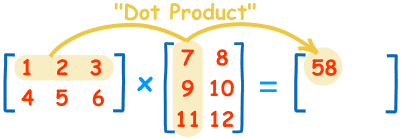
结果矩阵第 m 行与第 n 列交叉位置的那个值,等于第一个矩阵第 m 行与第二个矩阵第 n 列,对应位置的每个值的乘积之和。同时它只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义。
以下例子都是用二维刚体图形的变换来讲述。
二维刚体变换
Scale
我们可以使用下面的缩放矩阵来对一个二维图形进行缩放处理:
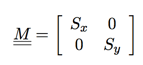 其中 Sx 和 Sy 分别为在 X 轴和 Y 轴上面的缩放因数,当一个点(x,y)T 和 M 进行矩阵相乘可以得到如下:
其中 Sx 和 Sy 分别为在 X 轴和 Y 轴上面的缩放因数,当一个点(x,y)T 和 M 进行矩阵相乘可以得到如下: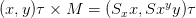 。
。
当 Sx=Sy=2 时,我们可以理解此转换矩阵可以将原图放大一倍,当=1/2,将原图缩放一倍,同时我们也可以通过 Scale 来进行反射,当 Sx=-1,Sy=1 时候,即可实现图形沿 Y 轴进行反射。
Skew
Skew 的意思是指扭曲,斜切变换,实现它的变换矩阵最简单的是这样的:
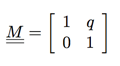
也即一个点[x,y]T 与它相乘可以得到: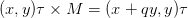 ,也即将点的 x 分量移动与其 y 分量成比例 q 的量。
,也即将点的 x 分量移动与其 y 分量成比例 q 的量。
一些稍微复杂的 Skew 如下所示,大家可以想想用 CSS3 中的 transform: skew 如何实现。
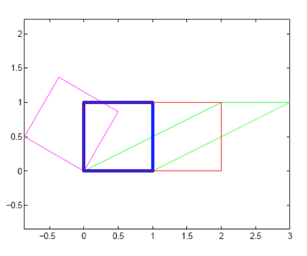
Rotation
我们可以通过下面那个选中矩阵对一个多边形沿逆时针方向旋转 θ 度:
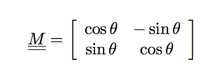
我们可以从下图看到一个点(1,0)T 围绕原点逆时针旋转了 θ 度,点的(1,0)T 拐角移动到点(cosθ,sinθ)T。